Xianwei Wang

Xianwei Wang, a native of Qufu, Shandong, is an associate professor in the School of Science at Zhejiang University of Technology. He received his PhD in June 2014 from the State Key Laboratory of Precision Spectroscopy at East China Normal University, and later joined Zhejiang University of Technology.

His education and work experience are as follows:

2005.09-2009.06: Bachelor's degree in Physics, Shandong Normal University

2009.09-2014.06: PhD in the State Key Laboratory of Precision Spectroscopy, East China Normal University

2014.06-2023.01: Lecturer, School of Science, Zhejiang University of Technology

2023.01-present: Associate Professor, School of Science, Zhejiang University of Technology.

Leading and Participating in Scientific Research Projects

Leading:

1)      Quantum Theoretical Study on Protein Design National Natural Science Foundation of China (NSFC) Young Scientist Fund, Jan 2018 - Dec 2020, with a direct funding of 210,000 RMB.

2)      Quantum Theoretical Calculations of Protein Electrostatic Properties and Vibrational Stark Spectroscopy NSFC Theoretical Physics Fund, Jan 2016 - Dec 2016, with a direct funding of 60,000 RMB.

3)      Application of Fragment-Based Quantum Chemistry Methods in Theoretical Design of Proteases Zhejiang Provincial Natural Science Foundation of China General Program, Jan 2017 - Dec 2019, with a direct funding of 80,000 RMB.

Participating:

4)      Study on Layered Heterostructures based on Bilayer Graphene and their Properties NSFC General Program, Jan 2020 - Dec 2023, with a direct funding of 540,000 RMB.

5)      Modeling of Surface Terminal Atom Distribution Characteristics and Simulation of Transport Properties of Two-dimensional Layered Ceramic Materials Zhejiang Provincial Natural Science Foundation of China General Program, Jan 2018 - Dec 2020, with a funding of 100,000 RMB.

Reviewer of Guangdong Provincial Natural Science Foundation

Reviewer of the journal Phys. Chem. Chem. Phys.

Research Interests:

Development of new methods:

1. Committed to advancing linear scaling quantum chemistry methods based on molecular fragmentization techniques, with the aim of facilitating their extensive utilization within large molecular systems

.

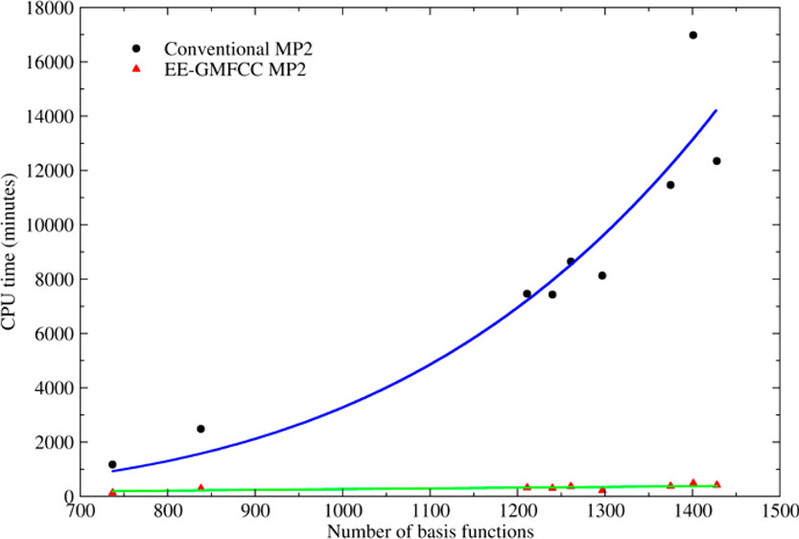
a) We have developed the EE-GMFCC (Electrostatically Embedded Generalized Molecular Fractionation with Conjugate Caps) method. This innovative approach not only ensures computational accuracy but also transforms the computational scaling of quantum chemical methods from exponential growth (where computational costs increase exponentially) to linear. As a result, this method has empowered the accurate computation of properties in protein systems containing thousands to tens of thousands of atoms using quantum chemical methods (see J. Phys. Chem. A 2013, 117(32): 7149-7161 https://doi.org/10.1021/jp400779t) 

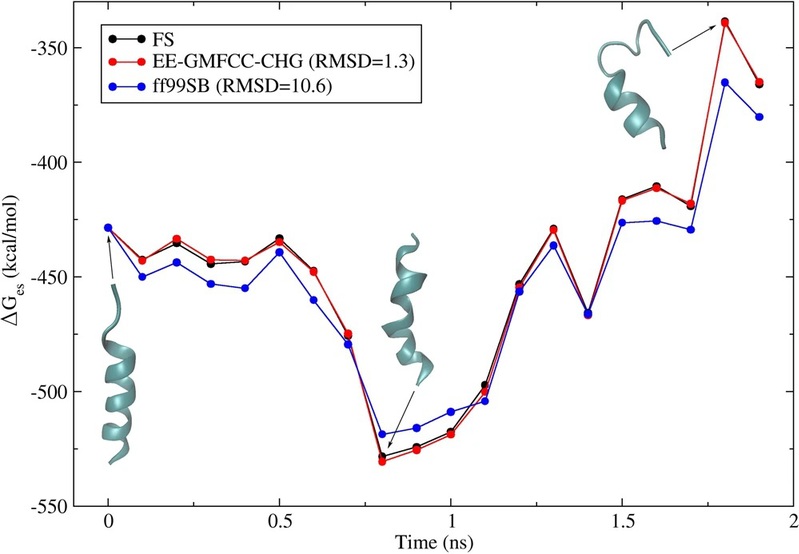
b)  The EE-GMFCC method can be utilized to precisely calculate the charge distribution within protein molecules, encompassing the Electrostatic Potential (ESP) charges. When integrated with an implicit solvent model grounded in the Poisson-Boltzmann equation (PB model), it is capable of delivering accurate predictions for the solvation energy of protein molecules (refer to Sci. Rep. 2018, 8, 5475 https://www.nature.com/articles/s41598-018-23783-8).

2.  A charge fitting method based on the analysis of electrostatic interaction energy has been proposed, known as the Electrostatic Energy-Based Charge Model (EEC charge model). This approach addresses the limitations of conventional fitting methods for Molecular Electrostatic Potential (ESP) charges, which can be overly sensitive to the electrostatic environment. Traditional ESP charges often require additional calculations to account for polarization effects, resulting in a significant increase in computational costs. The EEC method employs fixed charges to describe electrostatic interactions and offers slightly superior accuracy compared to polarizable ESP charges. This innovative methodology mitigates the excessive sensitivity of charge models to the electrostatic environment, ultimately enhancing computational efficiency. The EEC charge model can be harnessed to develop the next generation of more precise additive force fields, thereby bolstering our capacity to simulate and comprehend the properties of molecular systems.

    (In the application of biomolecular force fields, it is common to incorporate explicit water models. These water models, extensively employed in dynamic simulations such as TIP3P, TIP4P-Ew, TIP4P/2005, and others, have parameters (non-bonded interactions) that are empirically tuned based on experimental observations of water properties, including O-O radial distribution functions, evaporation enthalpy, density, and more. This empirical approach enables water models to accurately replicate various properties of water, making them generally effective in mimicking the behavior of real water molecules.

      However, in the realm of biomolecular force fields, non-bonded (electrostatic) interaction parameters are typically derived from first-principles calculations due to a shortage of adequate experimental data as reference points. For instance, some force fields utilize electrostatic potentials calculated from HF/6-31G* for molecules within the system (e.g., the RESP method in the Amber force field) or interactions between amino acid (DNA and RNA) residues and TIP3P water based on HF/6-31G* (e.g., the CHARMM force field) as benchmarks for charge derivation. While parameterization methods grounded in first principles calculations are straightforward, efficient, and user-friendly, it has been demonstrated that these parameterization approaches significantly deviate from the implicit physical approximations inherent in empirically adjusted parameterization schemes. This leads to some inconsistencies between the parameters obtained for biomolecular force fields and those of the water models, resulting in issues such as overestimation of protein-protein interactions during simulations and the emergence of compact conformations in simulations of naturally disordered proteins that deviate from experimental observations.

      Addressing this pressing issue necessitates exploring whether empirical parameter adjustment schemes, relying on experimental data as references, adhere to a more robust physical rationale beyond mere error cancellation. Additionally, it involves seeking a parameterization method based on first-principles calculations that exhibits deeper physical congruence with empirical parameterization methods.)

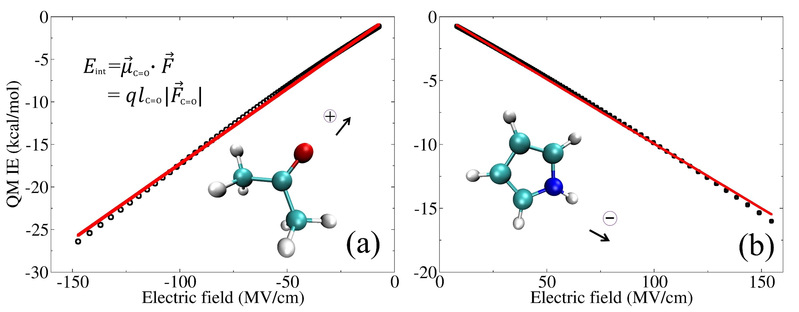
a)   It has been confirmed that there exists a general linear correlation between the QM/MM (Quantum Mechanics/Molecular Mechanics) interaction energy of polar chemical bonds and various external electric fields. This correlation highlights the feasibility of developing the Electrostatic Energy-Based Charge Model (EEC charge model) for polar chemical bonds based on the analysis of charge-electrostatic interaction energy. Furthermore, it has been demonstrated that, in simulations of internal electric fields within enzymes, charges fitted using this method can yield results that are more consistent with experimental measurements compared to traditional molecular force fields (see J. Chem. Phys. 2021, 154, 134107 https://doi.org/10.1063/5.0043707).

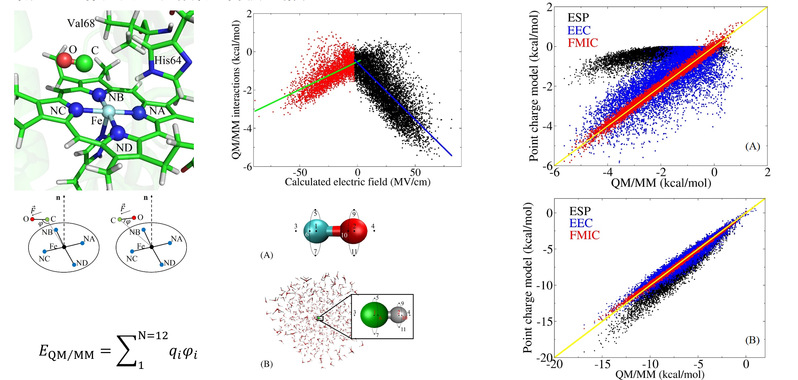
b)   Investigating carbon monoxide (CO) and hydrogen fluoride (HF) molecules, it has been confirmed that fixed numerical charge models (distinct from polarizable models, as they maintain constant charge values regardless of external environmental changes) can precisely predict the electrostatic interaction energies calculated through the QM/MM method when suitable interaction points are introduced around the molecules. The root mean square error (RMSE) for these charge models can be kept within 0.2 kcal/mol (see Phys. Chem. Chem. Phys. 2021, 23, 21001-21012 https://doi.org/10.1039/D1CP02776J)

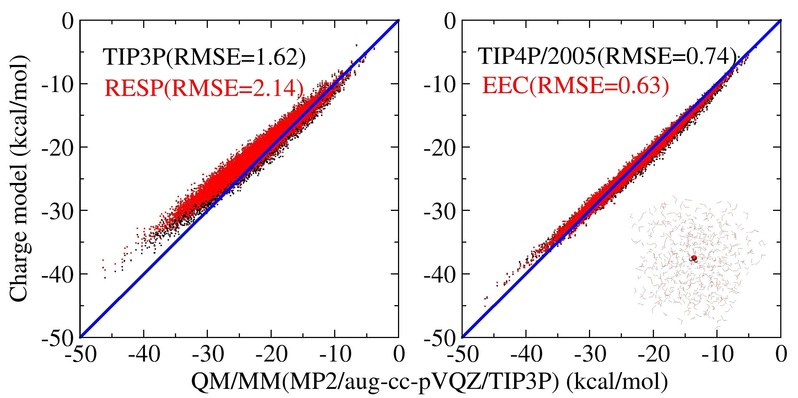
c)     Utilizing the RESP (Restrained Electrostatic Potential) method and the EEC (Electrostatic Energy-Based Charge) method, electrostatic models for water molecules were meticulously developed through first-principles calculations within a static-charge framework. These models were subsequently juxtaposed with charges derived from empirical adjustments grounded in experimental data for models such as TIP3P, TIP4P, TIP4P-Ew, and TIP4P/2005. Several noteworthy observations emerged:

※Fixed charge models provide an effective description of diverse electrostatic interactions among water molecules in the condensed phase. When compared to QM/MM calculations, they maintain a root mean square error (RMSE) under 0.6 kcal/mol, surpassing the conventional chemical accuracy threshold of 1 kcal/mol commonly aimed for in simulation studies.

※The method of empirically adjusting water model parameters, based on experimental observation data, aims to replicate observables like O-O radial distribution functions, density, and heat of vaporization for water. This approach not only relies on error cancellation among parameters but also places a strong emphasis on providing a better physical description of interactions among water molecules in the condensed phase.

※The RESP charge fitting approach demonstrates physical similarities with TIP3P in describing electrostatic interactions, while the EEC charge fitting approach shares akin physical characteristics with the more advanced TIP4P-Ew (as well as TIP4P/2005) water models. This implies that using the EEC model can enhance the precision of existing protein force fields to a level comparable to the TIP4P/2005 water model. By combining the EEC model with the TIP4P/2005 water model, it is possible to achieve a more balanced description of interactions among proteins, protein-water, and water-water.

These findings provide valuable insights into the physical relationships among different charge models and hold promise for establishing a stronger foundation for future force field development and molecular simulation research. (see J. Chem. Theory Comput. 2023, 19, 18, 6294–6312: https://doi.org/10.1021/acs.jctc.3c00467)

Applications:

(1) Computer-aided drug design

(2) High-throughput design of novel proteases

(3) Prediction of protein-protein interactions

(4) Study of vibration spectra and fluorescence spectra of biomolecules by combining molecular dynamics simulation and quantum chemistry calculation

(5) Study of the catalytic mechanism of proteases based on quantum mechanics/molecular mechanics (QM/MM) multiscale methods

More than 20 SCI papers have been published, including more than 10 first-author or corresponding author papers in international authoritative journals such as J. Chem. Phys., Phys. Chem. Chem. Phys., and Nature Communications.

Publications：

     (28)  Wang, X. W.*；Wang, Y.Y.; Guo, M.; Wang, X. C.; Li, Y.*; Zhang, J. Z. H.,  Assessment of an Electrostatic Energy-Based Charge Model for Modeling the Electrostatic Interactions in Water Solvent.  J. Chem. Theory Comput. 2023, 19, 18, 6294–6312.

(27) A. Hu, J.Z. Zhang, J. Wang, C.C. Li, M. Yuan, Z.C. Lin, Z.P. Qiu, H.Y. Liu, X.W. Wang, P.C. Wei, X. He, X.L. Zhao, W.W. Chou*, G. Deng and B.L. Song*, Cholesterylation of Smoothened is a calcium-accelerated autoreaction involving an intramolecular ester intermediate. Cell Research, 2022: 1-14. 

(26) Shen C.F.; Wang X.W.*; and He X.*, Fragment-based Quantum Mechanical Calculation of Excited-State Properties of Fluorescent RNAs. Front. Chem.  2021, 9, 801062. 

(25) Dai, D. H.#; Wang, X. W.#; Liu, Y. W.; Yang, X.-L.; Glaubitz, C.; Denysenkov, V.; He, X.*; Prisner, T.; Mao, J. F.*, Room-Temperature Dynamic Nuclear Polarization Enhanced Nmr Spectroscopy of Small Biological Molecules in Water. Nat. Commun. 2021, 12, 1-15.

(24) Wang, X. W.*; Li, X. L.; He, X.*; Zhang, J. Z. H.*, A Fixed Multi-Site Interaction Charge Model for an Accurate Prediction of the Qm/Mm Interactions. Phys. Chem. Chem. Phys. 2021, 23, 21001-21012. 

(23) Wang, X. W.*; Yan, J. H.; Zhang, H.; Xu, Z. S.; Zhang, J. Z. H.*, An Electrostatic Energy-Based Charge Model for Molecular Dynamics Simulation. J. Chem. Phys.2021, 154, 134107. 

(22) Wang, X. W.* ; Lu, C. H.; Yang M. Y.*, The Impact of Electron Correlation on Describing QM/MM Interactions in the Attendant Molecular Dynamics Simulations of CO in Myoglobin. Sci. Rep. 2020, 10,8539. 

(21) Lu, C. H.*; Chen, X.; Zhang, C.; Wang, X. W.; Li, S.; & Zhang, S. A., Controlling terahertz radiation in gas plasma with time-delayed laser pulses by the pulsing shaping technology. Optik, 2019, 185, 8-13. 

(20)Wang, X. W.*; Li, Y.; Gao, Y.; Yang, Z. J.; Lu, C. H.; Zhu, T.*, A quantum mechanical computational method for modeling electrostatic and solvation effects of protein. Sci. Rep. 2018, 8, 5475. 

(19)Wang, X. W.; He, X.*, An Ab Initio QM/MM Study of the Electrostatic Contribution to Catalysis in the Active Site of Ketosteroid Isomerase. Molecules 2018, 23, 2410.  

(18)Li, Y.; Wang, X. W.; Ren, L. L.; Cao, X.; Ji, C.; Xia, F.*; Zhang, J. Z. H.*, Electrostatic Polarization Effect on Cooperative Aggregation of Full Length Human Islet Amyloid. J. Chem. Inf. Model. 2018, 58, 1587-1595.  

(17)Pei, M.-J.; Lu, C.-H.*; Wang, X.-W.; Sun, Z.-R.; Zhang, S.-A., Enhancement and modulation of terahertz radiation by multi-color laser pulses. Chinese Physics B 2018, 27, 084209. (JCR 3区，IF=1.652)

(16)Wang, Y.; Wang, X. W.; Truhlar, D. G.*; He, X.*, How Well Can the M06 Suite of Functionals Describe the Electron Densities of Ne, Ne6+, and Ne8+? J. Chem. Theory Comput. 2017, 13, 6068-6077. 

(15)Wang, X. W.; Zhang, J. Z. H.; He, X.*, Ab initio Quantum Mechanics/Molecular Mechanics Molecular Dynamics Simulation of CO in the Heme Distal Pocket of Myoglobin. Chin. J. Chem. Phys. 2017, 30, 705-716. 

(14)Gao, Y.*; Zhang, C.; Wang, X. W.; Zhu, T.*, A test of AMBER force fields in predicting the secondary structure of alpha-helical and beta-hairpin peptides. Chem. Phys. Lett. 2017, 679, 112-118. 

(13) Cong, Y.; Li, M.; Feng, G.; Li, Y.; Wang, X. W.; Duan, L.*, Trypsin-Ligand binding affinities calculated using an effective interaction entropy method under polarized force field. Sci. Rep. 2017, 7, 1-12. 

(12) Duan, L.*; Feng, G.; Wang, X. W.; Wang, L.; Zhang, Q., Effect of electrostatic polarization and bridging water on CDK2-ligand binding affinities calculated using a highly efficient interaction entropy method. Phys. Chem. Chem. Phys. 2017, 19, 10140-10152. 

(11) Yang, Z.-J.*; Gao, Q.-H.; Xiong, H.-N.; Shao, J.-X.; Wang, X.-W.; Xu, Z.-J., Pressure-induced magnetic moment abnormal increase in Mn2FeAl and non-continuing decrease in Fe2MnAl via first principles. Sci. Rep. 2017, 7, 1-9. 

(10) Lu, C. H.*; Zhang, C.; Zhang, L.; Wang, X. W.; Zhang, S. A.*, Modulation of terahertz-spectrum generation from an air plasma by tunable three-color laser pulses. Phys. Rev. A 2017, 96,053402. 

(9) Wang, X. W.; He, X.*; Zhang, J. Z. H.*, Accurate Calculation of Electric Fields Inside Enzymes. Methods in Enzymology, 2016; Vol. 578; pp 45-72.

(8) Wang, X. W.; Zhang, J. Z. H.*; He, X.*, Quantum mechanical calculation of electric fields and vibrational Stark shifts at active site of human aldose reductase. J. Chem. Phys. 2015, 143, 184111.

(7) Liu, J.; Wang, X. W.; Zhang, J. Z. H.*; He, X.*, Calculation of protein-ligand binding affinities based on a fragment quantum mechanical method. Rsc. Advances 2015, 5, 107020-107030.

(6) Liu, J.; Zhu, T.; Wang, X. W.; He, X.*; Zhang, J. Z. H.*, Quantum Fragment Based ab Initio Molecular Dynamics for Proteins. J. Chem. Theory Comput. 2015, 11, 5897-5905. 

(5) He X.*; Zhu T.; Wang X. W.; et al., Fragment quantum mechanical calculation of proteins and its applications[J]. Accounts Chem. Res.,2014, 47(9): 2748-2757. 

(4) Wang X. W.; Li Y. X.; He X.*; et al., Effect of strong electric field on the conformational integrity of insulin[J]. J. Phys. Chem. A 2014, 118(39): 8942-8952.

(3) Jia X. Y., Wang X. W., Liu J. F., et al. An improved fragment-based quantum mechanical method for calculation of electrostatic solvation energy of proteins[J]. J. Chem. Phys. 2013,, 139(21): 12B604_1. 

(2)Wang, X. W.; He X.*; Zhang J. Z. H.*, Predicting mutation-induced Stark shifts in the active site of a protein with a polarized force field. J. Phys. Chem. A 2013,117, 6015-6023. 

(1) Wang X. W., Liu J. F., Zhang J. Z. H.*, et al. Electrostatically embedded generalized molecular fractionation with conjugate caps method for full quantum mechanical calculation of protein energy[J]. J. Phys. Chem. A 2013, 117(32): 7149-7161.